更新于:2023-12-04 15:30
一、定理介绍
四色定理:是世界近代三大数学难题之一,又称四色猜想、四色问题,是一个著名的数学定理。它对应的四色问题是:如果在平面上划出一些邻接的有限区域,那么可以用四种颜色来给这些区域染色,使得每两个邻接区域染的颜色都不一样。另一个通俗的说法是:每个无外飞地的地图都可 以用不多于四种颜色来染色,而且不会有两个邻接的区域颜色相同。被称为邻接的两个区域是指它们有一段公共的边界,而不仅仅是一个公共的交点。
二、使用背景
将 word 中表格进行染色,保证相邻的单元格的颜色不同。
上面描述的是一个很神奇的需求,如果表格是一个正常的 m * n 列的,其实两种颜色便可以满足了。
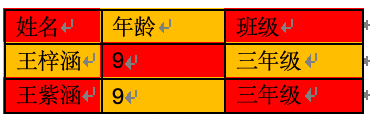
但是考虑到实际当中存在单元格合并的场景,两种甚至三种颜色都不一定能够满足要求。因此就需要把一个表格看成一张地图,每个完整的单元格都是一个国家,为了把单元格区分出来就需要对其染色,因此就需要四色定理来处理。
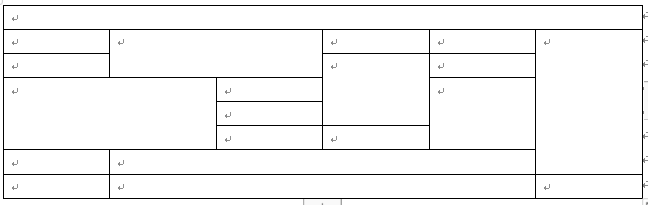
大家可以自己动手试试,能不能用不超过三个数字填满上面表格中的单元格,需要保证相邻单元格数字不重复。
三、逻辑实现
填色的算法采用比较简单的思路(递归和回溯),不断地尝试所有可能的方案,只要遇到一个可以填完颜色的方案为止。具体步骤如下:
1、获取单元格的合并信息;
2、检查当前区域所有可以使用的颜色(查看自己邻接的区域都用了哪些颜色,没被使用过的就是自己可以用的);
3、如果当前区域没有颜色可以使用,则返回失败给上一层,上一层则会尝试换一种颜色;
4、从当前区域可使用的颜色中,逐个尝试,如果下一层一直迭代到最后填色成功,则整体填色成功,否则,就换个颜色继续尝试;
5、递归重复 2、3、4 步骤直到完成任务。
def get_color_map(map_info_list):
def get_value(x, y):
if x < 0 or x >= row_count or y < 0 or y >= col_count:
return -1
return map_info_list[x][y]
def add_neighbor(x, y, neighbors):
val = map_info_list[x][y]
if val == -1:
return
if val not in neighbors:
neighbors[val] = set()
neighbors[val].add(get_value(x, y + 1))
neighbors[val].add(get_value(x, y - 1))
neighbors[val].add(get_value(x - 1, y))
neighbors[val].add(get_value(x + 1, y))
def coloring(level):
if level > len(neighbors):
return True
neighbor = neighbors[level]
colors = set(color_map_dict[n] for n in neighbor if n != -1 and color_map_dict[n] > 0)
if len(colors) == 4:
return False
for i in range(1, 5):
if i not in colors:
color_map_dict[level] = i
if coloring(level + 1):
return True
color_map_dict[level] = 0
return False
color_map_dict, neighbors = {}, {}
row_count = len(map_info_list)
col_count = len(map_info_list[0])
for row_idx in range(0, row_count):
for col_idx in range(0, col_count):
add_neighbor(row_idx, col_idx, neighbors)
for neighbor_idx in range(0, len(neighbors)):
color_map_dict[neighbor_idx + 1] = 0
color_map_dict[1] = 1
coloring(2)
return color_map_dict
if __name__ == '__main__':
print("下面每个数字表示单元格的序号,合并单元格的序号会一致")
cell_merge_info_1 = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
]
map_info_1 = get_color_map(cell_merge_info_1)
if len(set(map_info_1.values())) != 2:
raise Exception()
cell_merge_info_2 = [
[1, 1, 1, 1, 1, 1],
[2, 3, 3, 4, 5, 6],
[7, 3, 3, 8, 9, 6],
[10, 10, 11, 8, 12, 6],
[10, 10, 13, 8, 12, 6],
[10, 10, 14, 15, 12, 6],
[16, 17, 17, 17, 17, 6],
[18, 19, 19, 19, 19, 20],
]
map_info_2 = get_color_map(cell_merge_info_2)
if len(set(map_info_2.values())) != 4:
raise Exception()
四、小结
本篇文章首先介绍了四色定理,通过需求引入为什么需要四色定理,最后通过递归法和回溯法来实现表格中单元格的染色。